https://m.blog.naver.com/tjdrud1323/221720259834
PCA(주성분 분석)_Python(파이썬) 코드 포함
PCA PCA는 무엇이며 언제 사용하는가? https://www.youtube.com/watch?v=FgakZw6K1QQ P...
blog.naver.com
https://www.youtube.com/watch?v=jNwf-JUGWgg
공분산 행렬
- 공분산 행렬의 의미: 각 feature의 변동이 얼마나 닮았나?
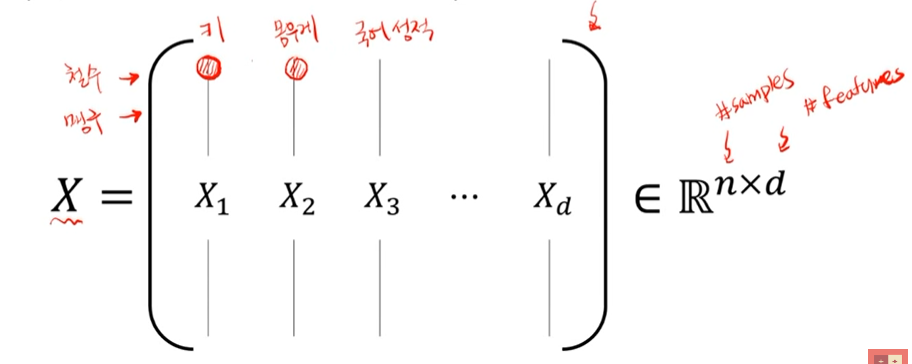
- 각 feature에서 평균을 뺀 값 : 변동
- 닮은 정도를 알기 위해서는 키의 변동, 몸무게의 변동에 내적을 적용.
-> 두 매트릭스 곱해주면 분산, 공분산으로 이루어진 symmatric matrix가 만들어지게 됨


- n이 아니라 n-1으로 나눠주기도 하는데, sample이 많으면 상관없음.
- 공분산 행렬은 선형 변환의 의미도 가짐. (shearing: 잡아당김)
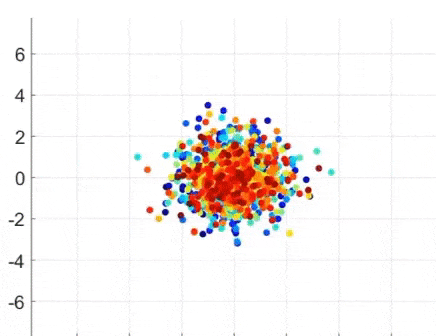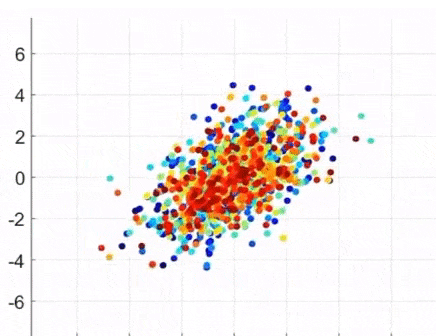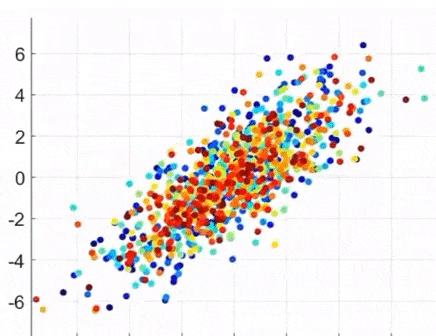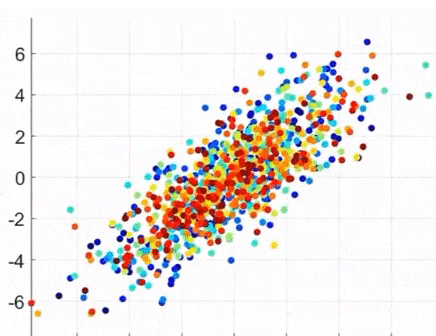
PCA (Principal Component Analysis)
: 공분산 행렬의 eigenvector
- 데이터의 구조를 잘 살려주면서 차원 감소를 할 수 있게끔 하는 방법
- 2차원 평면 상의 산점도를 1차원에 정사영시켜 차원을 감소 -> 어떤 벡터에 정사영시키는 것이 가장 좋을지 찾는 과정
- 키, 몸무게, 영어, 국어, 수학, 과학 -> 신체적 능력, 문과적 능력, 이과적 능력의 3차원으로 줄이는 것.
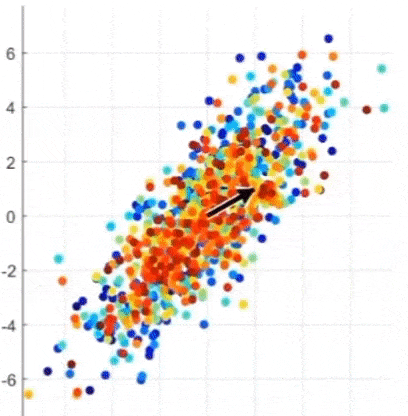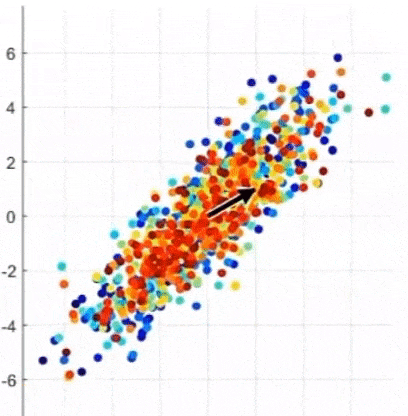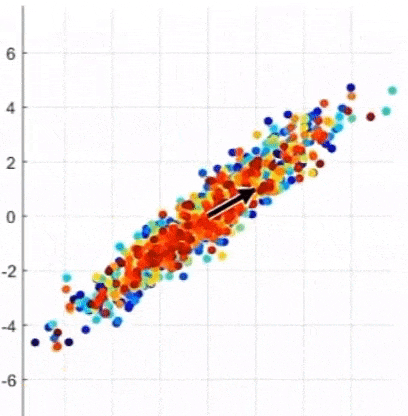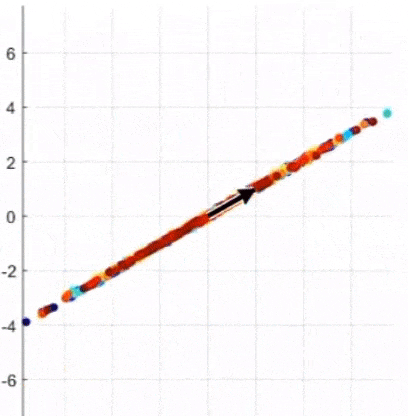
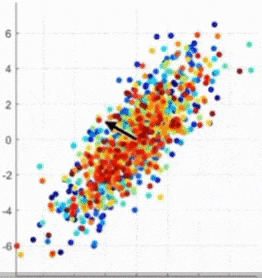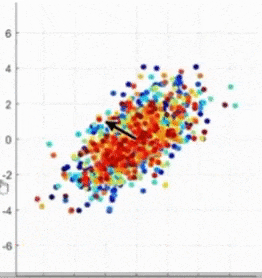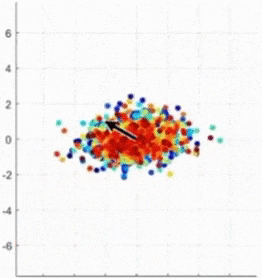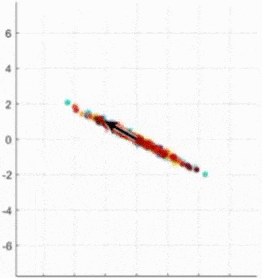
- 어떤 것이 Principal Axis인가? (4.XX vs. 0.89)
-> 정사영 후의 데이터 분포의 분산이 가장 큰 것, 주축(=eigenvector)에 대해 정사영 하는 것이 가장 좋다
-> Eigenvector 찾기 = 선형변환을 했을 때 크기만 바뀌고 방향은 바뀌지 않는 벡터 찾기
- 3차원 데이터에서는 3개의 eigenvector 나오고, 이 중 eigenvalue가 큰 두 개가 이루는 평면에 데이터 정사영
'Computer > ML·DL·NLP' 카테고리의 다른 글
| [KoBigBird] Basemodel, configuration (0) | 2022.12.16 |
|---|---|
| [ML] train, valid, test batch size 조정하기, 그 영향 (1) | 2022.12.06 |
| [ML] 머신러닝 모델에서의 head, backbone이란? (0) | 2022.08.29 |
| Sequential Model 이란? (0) | 2022.07.01 |
| [스크랩] jaehyeong 님의 Basic NLP (0) | 2022.06.27 |

댓글